A Square and A Cube Class 8 Solutions Ganita Prakash Maths Chapter 1 - #NCSOLVE 📚

Solving questions with the help of Ganita Prakash Class 8 Solutions and Class 8 Maths Chapter 1 A Square and A Cube NCERT Solutions Question Answer improves confidence.

NCERT Class 8 Maths Chapter 1 A Square and A Cube Solutions Question Answer

Ganita Prakash Class 8 Chapter 1 Solutions A Square and A Cube

NCERT Class 8 Maths Ganita Prakash Chapter 1 A Square and A Cube Solutions Question Answer

NCERT Intext Questions

Question 1.
Find the squares of the first 30 natural numbers and fill in the table below. (Page 4)

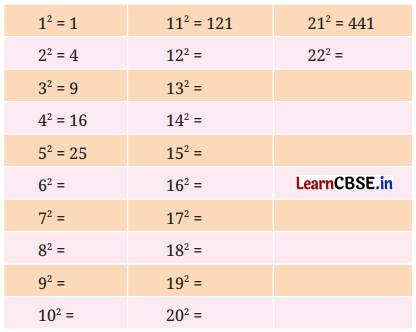
Solution:

Question 2.
What patterns do you notice? Share your observations and make conjectures. (Page 4)
Solution:
In the above sequence, we notice that the sum of consecutive odd numbers is a perfect square.
We see that the next perfect square is the sum of the next consecutive odd number.
Observation:
1² = 1
2² = 1 + 3 = 4
3² = 1 + 3 + 5 = 9
4² = 1 + 3 + 5 + 7 = 16
5² = 16 + 9 = 25
6² = 25 + 11 = 36
7² = 36 + 13 = 49
.
.
.
.
28² = 729 + 55 = 784
29² = 784 + 57 = 841
30² = 841 + 59 = 900

Question 3.
Which of the following numbers has the digit 6 in the units place? (Page 5)
(i) 38²
(ii) 34²
(iii) 46²
(iv) 56²
(v) 74²
(vi) 82²
Solwer:
We know if a number has 4 or 6 in the units place, then its square ends in 6.
So, squares of (ii) 34, (iii) 46, (iv) 56, and (v) 74 have the digit 6 in the units place.

Question 4.
Find more such patterns by observing the numbers and their squares from the table you filled earlier. (Page 5)
Solution:
If a number has a 3 or 9 in the units place, its square will always end in 6.
If a number has a 2 or 8 in the units place, its square will always end in 4.
If a number has a 5 in the units place, its square will always end in 5.

Question 5.
If a number contains 3 zeros at the end, how many zeros will its square have at the end? (Page 5)
Solution:
If a number contains 3 zeros at the end, then its square will have 6 zeros at the end.

Question 6.
What do you notice about the number of zeros at the end of a number and the number of zeros at the end of its square? Will this always happen? Can we say that squares can only have an even number of zeros at the end? (Page 5)
Solution:
We noticed that the number of zeros at the end of its square has doubled.
Yes, it will always happen.
And also, we can say that squares can only have an even number of zeros at the end.

Question 7.
What can you say about the parity of a number and its square? (Page 5)
Solution:
We say that when a number is multiplied by itself, it is called its square.

Figure It Out (Pages 10-11)

Question 1.
Which of the following numbers are not perfect squares?
(i) 2032
(ii) 2048
(iii) 1027
(iv) 1089
Solution:
(i) 2032 is not a perfect square, as a number ending with 2 can not be a perfect square.
(ii) 2048 is not a perfect square, as a number ending with 8 can not be a perfect square.
(iii) 1027 is not a perfect square, as a number ending with 7 can not be a perfect square.
(iv) 1089 ends in 9 at the unit’s place. Hence, it is a perfect square.

Question 2.
Which one among 64², 108², 292², 36² has the last digit 4?
Solution:
(i) Unit’s digit of 64 is 4
∴ 4² = 4 × 4 = 16 (last digit = 6)
(ii) Unit’s digit of 108 is 8
∴ 8² = 8 × 8 = 64 (last digit = 4)
(iii) Unit’s digit of 292 is 2
∴ 2² = 2 × 2 = 4
(iv) Unit’s digit of 36 = 6
∴ 6² = 6 × 6 = 36 (last digit = 6)
Hence, the numbers whose squares end in 4 are 108² and 292².

Question 3.
Given 125² = 15625, what is the value of 126²?
(i) 15625 + 126
(ii) 15625+ 26²
(iii) 15625 + 253
(iv) 15625 + 251
(v) 15625 + 51²
Solution:
Here, 126² = (125 + 1)²
= (125)² + 2 × 125 × 1 + (1)² [Using identity (a + b)² = a² + 2ab + b²]
= 15625 + 250 + 1
= 15625 + 251
So, the value of 126² is (iv) option, i.e., 15625 + 251.

Question 4.
Find the length of the side of a square whose area is 441 m².
Solution:

Area of square = side × side = 441
⇒ side² = 441
⇒ side = √441
441 = 3 × 3 × 7 × 7
√444 = 3 × 7 = 21
∴ Side of square = 21 m.

Question 5.
Find the smallest square number that is divisible by each of the following numbers: 4, 9, and 10.
Solution:
To find the required smallest square number, we will find the least number divisible by each of 4, 9, and 10, i.e., LCM of 4, 9, and 10.

LCM = 2 × 2 × 3 × 3 × 5 = 180
Prime factorisation of 180 = 2 × 2 × 3 × 3 × 5
5 is not in pairs, so 180 is not a square number.
In order to get a perfect square, we will multiply 180 by 5.
So, the required smallest square number is 900.

Question 6.
Find the smallest number by which 9408 must be multiplied so that the product is a perfect square. Find the square root of the product.
Solution:

9408 = 2 × 2 × 2 × 2 × 3 × 3 × 3 × 7 × 7
All prime factors of 9408 are arranged in pairs except 3.
So, we multiply 9408 by 3 to make it a perfect square.
Perfect square = 9408 × 3 = 28224
Now, \(\sqrt{28224}=\sqrt{2 \times 2 \times 2 \times 2 \times 3 \times 3 \times 3 \times 3 \times 7 \times 7}\)
= 2 × 2 × 3 × 3 × 7
= 252

Question 7.
How many numbers lie between the squares of the following numbers?
(i) 16 and 17
(ii) 99 and 100
Solution:
(i) Numbers lying between 16² and 17² = 2 × 16 = 32
(ii) Numbers lying between 99² and 100² = 2 × 99 = 198

Question 8.
In the following pattern, fill in the missing numbers:
1² + 2² + 2² = 3²
2² + 3² + 6² = 7²
3² + 4² + 12² = 13²
4² + 5² + 20² = (__)2
9² + 10² + (__)2 = (__)2
Solution:
1² + 2² + 2² = 3²
2² + 3² + 6² = 7²
3² + 4² + 12² = 13²
4² + 5² + 20² = (21)²
9² + 10² + (90)² = (91)²

Question 9.
How many tiny squares are there in the following picture? Write the prime factorisation of the number of tiny squares.

Solution:
Big squares in a row = 9
Big squares in a column = 9
Tiny squares in a big square = 25
∴ Total tiny squares = 9 × 9 × 25 = 2025
Now prime factorisation of 2025 = 3 × 3 × 3 × 3 × 5 × 5 = 452

Figure It Out (Pages 16-17)

Question 1.
Find the cube roots of 27000 and 10648.
Solution:
Here,

∴ 27000 = 2 × 2 × 2 × 3 × 3 × 3 × 5 × 5 × 5
∴ \(\sqrt[3]{27000}\) = 2 × 3 × 5 = 30

∴ 10648 = 2 × 2 × 2 × 11 × 11 × 11
∴ \(\sqrt[3]{10648}\) = 2 × 11 = 22

Question 2.
What number will you multiply by 1323 to make it a cube number?
Solution:
Here,

1323 = 3 × 3 × 3 × 7 × 7
To complete the triplet, one more 7 is required.
So, 1323 will be multiplied by 7 to make it a cube number.
So, the cube number = 1323 × 7 = 9261
Hence, required number = 7

Question 3.
State true or false. Explain your reasoning.
(i) The cube of any odd number is even.
(ii) There is no perfect cube that ends with 8.
(iii) The cube of a 2-digit number may be a 3-digit number.
(iv) The cube of a 2-digit number may have seven or more digits.
(v) Cube numbers have an odd number of factors.
Solution:
(i) The cube of any odd number is even. (False)
Reason: The cube of an odd number is always odd, as
3³ = 27
5³ = 125
7³ = 343

(ii) There is no perfect cube that ends with 8. (False)
Reason: The cubes of all the numbers ending with 2 at the unit place end with 8.
2³ = 8
12³ = 1728
22³ = 10648

(iii) The cube of a 2-digit number may be a 3-digit number. (False)
Reason: Cube of a 2-digit number may have a minimum of 4 digits to a maximum of 6 digits.
10 is the smallest 2-digit number, and 10³ = 1000, which has 4 digits.

(iv) The cube of a 2-digit number may have seven or more digits. (False)
Reason: Cube of a 2-digit number may have at most 6 digits.
99 is the largest 2-digit number, and 99³ = 970299, which is a 6-digit number.

(v) Cube numbers have an odd number of factors. (False)
Reason: Cube numbers may have an odd as well as an even number of factors.
As 27 = 3 × 3 × 3 (odd no. of factors)
64 = 2 × 2 × 2 × 2 × 2 × 2 (even no. of factors)

Question 4.
You are told that 1331 is a perfect cube. Can you guess without factorisation what its cube root is? Similarly, guess the cube roots of 4913, 12167, and 32768.
Solution:
To find the cube root of 1331
1331
We divide the given number 1331 into two groups, starting from the right side, taking three digits in group 1.
331 → group 1
1 → group 2
331 → unit digit is 1
Hence, the cube roots of one’s digit is 1 …..(1)
Group 2, i.e., 1 only, which is 1³.
So, the cube roots of one’s digit is 1. ……(2)
∵ \(\sqrt[3]{1331}\) = 11

4913
Group 1 – 913
Group 2 – 4
Unit digit of 913 is 3.
We know that 3 comes at the unit’s place when its cube root ends in 7, as 7 × 7 × 7 = 343
So the unit digit of the cube root of 4913 = 7 …..(1)
Group 2 – 4
4 lies between 1 (i.e., 13) and 23 (i.e., 8)
1³ < 4 < 2³
Taking the lower limit, the tens digit of the cube root of 4913 is 1. …..(2)
\(\sqrt[3]{4913}\) = 17 (from (1) & (2))

12167
Group 1 – 167
Unit digit = 7
So unit digit of cube root of 12167 = 3 as 3 × 3 × 3 = 27
Group 2 – 12
8 < 12 < 27
2³ < 12 < 3³
Taking the lower limit, the ten’s digit of cube root = 2
So \(\sqrt[3]{12167}\) = 23

32768
Group 1 – 768
Unit digit = 8
So unit digit of cube root of 32768 = 2 …..(1)
as 2 × 2 × 2 = 8
⇒ \(\sqrt[3]{8}\) = 2
From Group 2 – 32
27 < 32 < 64
3³ < 32 < 4³
Taking lower limit, ten’s digit of the cube root of 32768 is 3. …..(2)
∴ \(\sqrt[3]{32768}\) = 32 (from (1) & (2))

Question 5.
Which of the following is the greatest? Explain your reasoning.
(i) 67³ – 66³
(ii) 43³ – 42³
(iii) 67² – 66²
(iv) 43² – 42²
Solution:
(i) 67³ – 66³ = 1 + 67 × 66 × 3
(ii) 43³ – 42³ = 1 + 43 × 42 × 3
(iii) 67² – 66² = 67 + 66 = 133
(iv) 43² – 42² = 43 + 42 = 85
From above we can see that 67³ – 66³ is the greatest as
(n + 1)³ – n³ = 1 + (n + 1) × 3n
(n + 1)² – n² = n + n + 1 = 2n + 1

The post A Square and A Cube Class 8 Solutions Ganita Prakash Maths Chapter 1 appeared first on Learn CBSE.

📚 NCsolve - Your Global Education Partner 🌍

Empowering Students with AI-Driven Learning Solutions

Welcome to NCsolve — your trusted educational platform designed to support students worldwide. Whether you're preparing for Class 10, Class 11, or Class 12, NCsolve offers a wide range of learning resources powered by AI Education.

Our platform is committed to providing detailed solutions, effective study techniques, and reliable content to help you achieve academic success. With our AI-driven tools, you can now access personalized study guides, practice tests, and interactive learning experiences from anywhere in the world.

🔎 Why Choose NCsolve?

At NCsolve, we believe in smart learning. Our platform offers:

• ✅ AI-powered solutions for faster and accurate learning.
• ✅ Step-by-step NCERT Solutions for all subjects.
• ✅ Access to Sample Papers and Previous Year Questions.
• ✅ Detailed explanations to strengthen your concepts.
• ✅ Regular updates on exams, syllabus changes, and study tips.
• ✅ Support for students worldwide with multi-language content.

🌐 Explore Our Websites:

🔹 ncsolve.blogspot.com
🔹 ncsolve-global.blogspot.com
🔹 edu-ai.blogspot.com

📲 Connect With Us:

👍 Facebook: NCsolve
📧 Email: ncsolve@yopmail.com

#NCsolve #EducationForAll #AIeducation #WorldWideLearning #Class10 #Class11 #Class12 #BoardExams #StudySmart #CBSE #ICSE #SamplePapers #NCERTSolutions #ExamTips #SuccessWithNCsolve #GlobalEducation