CBSE Sample Papers for Class 10 Maths Standard Set 4 with Solutions - #NCSOLVE 📚

Students must start practicing the questions from CBSE Sample Papers for Class 10 Maths Standard with Solutions Set 4 are designed as per the revised syllabus.

CBSE Sample Papers for Class 10 Maths Standard Set 4 with Solutions

Time : 3 Hrs
Max. Marks: 80

General Instructions
Read the following instructions carefully and follow them.

1. This question paper contains 38 questions. All questions are compulsory.
2. This question paper is divided into 5 section A, B, C, D and E.
3. In Section A, question numbers 1-18 are Multiple Choice Questions (MCQs) and question number 19 and 20 are Assertion-Reason based questions of 1 mark each.
4. In Section B, question numbers 21-25 are Very Short Answer (VSA) type questions, carrying 02 marks each.
5. In Section C, question numbers 26-31 are Short Answer (SA) type questions, carrying 03 mark each.
6. in Section b, question numbers 32-35 are Long Answer (LA) type questions, carrying 05 marks each.
7. In Section E, question numbers 36-38 are Case Study Based questions carrying 4 marks each with sub parts of the values 1,1 and 2 marks each respectively.
8. There is no overall choice. However, an internal choice in 2 questions of section B, 2 questions of section C and 2 questions of section D has been provided. An internal choice has been provided in all the 2 marks questions of section E.
9. Draw neat and clear figures wherever required. Take it π = \(\frac{22}{7}\) wherever required if not stated.
10. Use of calculators is not allowed.

Section – A
Multiple Choice Questions (Each Question carries 1 M)

Question 1.
In a ∆ABC, Dand Eare points on the sides ABand AC respectively such that DE ∥ BC If = \(\frac{A D}{D B}=\frac{2}{3}\) and AC = 18cm, then the value of AE is
(a) 5 cm
(b) 6.2 cm
(c) 8 cm
(d) 7.2 cm
Answer:
(d) 7.2 cm

Explanation:
Given, DE ∥ BC, \(\frac{A D}{D B}=\frac{2}{3}\) and AC = 18 cm DB 3

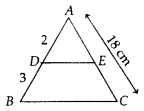
In ∆ABC, DE ∥ BC
∴ \(\frac{A D}{D B}=\frac{A E}{E C}\)
[by basic proportionality theorem]
⇒ \(\frac{2}{3}=\frac{A E}{18-A E}\) [∵ \(\frac{A D}{D B}=\frac{2}{3}\)]
⇒ \(\frac{2}{3}=\frac{A E}{18-A E}\)
⇒ 36 – 2AE = 3AE
⇒ 36 = 5AE
⇒ AE = \(\frac {36}{5}\) = 7.2 cm

Question 2.
If sec θ = \(\frac{17}{8}\), then cot θ is
(a) \(\frac{8}{17}\)
(b) \(\frac{15}{17}\)
(c) 2
(d) \(\frac{8}{15}\)
Answer:
(d) \(\frac{8}{15}\)

Explanation:
Given, sec θ = \(\frac{17}{8}=\frac{\text { hypotenuse }}{\text { base }}\)

In ∆ABC, by Pythagoras theorem, we get
(AB)² + (BC)² = (AC)²
⇒ (AB)² = (AC)² – (BC)²
⇒ AB = \(\sqrt{(17)^2-(8)^2}=\sqrt{289-64}=\sqrt{225}\)
∴ AB = 15

Now, cot θ = \(\frac{\text { Base }}{\text { Perpendicular }}\)
⇒ cot θ = \(\frac{B C}{A B}\)
⇒ cot θ = \(\frac{8}{15}\)

Question 3.
In the following figure, the value of ∠F is

(a) 0°
(b) 30°
(c) 45°
(d) 60°
Answer:
(d) 60°

Explanation:
In ∆ABC and ∆DEE,
\(\frac{A B}{D F}=\frac{B C}{F E}=\frac{C A}{E D}=\frac{1}{2}\)
By SSS criterion of similarity, we have
∆ABC ~ ∆DFE
Then, ∠A = ∠D, ∠B = ∠F and ∠C = ∠E [∵ ∠B = 60°]
∴ ∠F = 60°

Question 4.
Prime factorisation of the number 98 is
(a) 2
(b) 2 × 7³
(c) 7²
(d) 2 × 7²
Answer:
(d) 2 × 7²

Explanation:
Factor tree is as follows.

∴ Prime factorisation of 98 = 2 × 7 × 7 = 2 × 7²

Question 5.
A tower stands near an airport. The angle of elevation θ of the tower from a point on the ground is such that its tangent is \(\frac{5}{12}\). The height of the tower, if the distance of the observer from the tower is 120 m is
(a) 60 m
(b) 50 m
(c) 40 m
(d) None of these
Answer:
(b) 50 m

Explanation:
Let BC = h m be the height of the tower and let A be the point on the ground such that AB = 120 m and ∠BAC = θ.

In right angled ∆ABC, we have
tan θ = \(=\frac{B C}{A B}=\frac{h}{120}\) [∵ tan = \(\frac{\text { perpendicular }}{\text { base }}\)]
⇒ \(\frac{5}{12}=\frac{h}{120}\) [∵ tan = \(\frac{5}{12}\), given]
∴ h = \(\frac{5 \times 120}{12}\) = 5 × 10 =- 50 m
Hence, the height of the tower is 50 m.

Question 6.
The distance between A(- 5, 3) and B(- 2, -1) is
(a) 4
(b) 9
(c) \(\sqrt{53}\)
(d) 5
Answer:
(d) 5

Explanation:
Given, coordinates of point A =(- 5,3) and coordinates of point B = (- 2, -1)
We know that the distance between two points (x₁, y₁) and(x₂, y₂)
= \(\sqrt{\left(x_1-x_2\right)^2+\left(y_1-y_2\right)^2}\)
Distance between A and B,
AB = \(=\sqrt{(-2+5)^2+(-1-3)^2}\)
= \(\sqrt{(3)^2+(-4)^2}\)
= \(\sqrt{9+16}=\sqrt{25}\)
= 5 units
[∵ distance cannot be negative]

Question 7.
If four vertices of a parallelogram taken in order are (-3, -1) (a, b), (3, 3) and (4, 3), then a: bis equal to
(a) 1 : 4
(b) 4 : 1
(c) 1 : 2
(d) 2 : 1
Answer:
(b) 4 : 1

Explanation:
Let vertices of paralellogram are A(-3, -1), B(a, b), C(3, 3) and D(4, 3), respectively. Then,

Coordinates of the mid-point of AC = Coordinates of the mid-point of BD [∵ in parallelogram, diagonals bisect each other]
⇒ \(\left(\frac{-3+3}{2}, \frac{-1+3}{2}\right)\) = \(\left(\frac{a+4}{2}, \frac{b+3}{2}\right)\)
⇒ (0, 1) = \(\left(\frac{a+4}{2}, \frac{b+3}{2}\right)\)
⇒ \(\frac{a+4}{2}\) = 0 and \(\frac{b+3}{2}\) = 1
⇒ a = -4 and b = -1
Now, \(\frac{a}{b}=\frac{-4}{-1}=\frac{4}{1}\)
⇒ a : b = 4 : 1

Question 8.
The length of minute hand of a clock is 10.5 cm. Then, the area swept by the minute hand in 15 minutes is
(a) 86.625 cm²
(b) 66.625 cm²
(c) 80.625 cm²
(d) 5.70 cm²
Answer:
(a) 86.625 cm²

Explanation:
The minute hand of a clock describes a circle of radius equal to its length i.e. 10.5 cm. So, the angle described by minute hand in 60 min = 360°.
Then, angle described by minute hand in 15 min
= \(\frac{360^9}{60}\) × 15 = 90°

So, the area swept by the minute hand in 15 min is the area of a sector of angle 90° in a circle of radius 10.5 cm. 0
∴ Required area = \(\frac{\theta}{360^{\circ}}\) × πr²
= \(\frac{90^{\circ}}{360^{\circ}} \times \frac{22}{7}\) × 10.5 × 10.5
= 86.625 cm²

Question 9.
If Σf_i is the sum of frequency and it is equal to the sum of first 10 natural numbers and ’Σf_ix_i = 120, then the mean is
(a) 2
(b) 0
(c) 2.18
(d) 1.18
Answer:
(c) 2.18

Explanation:
Given, Σf_i = 1 + 2 + … + 10
= \(\frac{10}{2}\)[2 × 1 + (10 – 1) × 1]
[∵ S_n = \(\frac{n}{2}\)n[2a + (n – 1)d]
= 5[2 + 9]
= 55
Mean, x̄ = \(\frac{\Sigma f_i x_i}{\Sigma f_i}=\frac{120}{55}\) = 2.18 [given, Σf_ix_i = 120]

Question 10.
If tangents PA and PB.from a point P to a circle with centre O are inclined to each other at angle of 60°, then the value of ∠POA is
(a) 50°
(b) 90°
(c) 0°
(d) 60°
Answer:
(d) 60°

Explanation:
We know that OA ⊥ AP
[tangent is perpendicular to the radius at the point of contact]
⇒ ∠OAP = 90°

and ∠APO = \(\frac{1}{2}\)∠APB
[∵ the centre of a circle lies on the bisector of the angle between the two tangents]
= \(\frac{1}{2}\) × 60° = 30°

In ∆PAO, ∠OAP + ∠APO + ∠POA = 180°
[by angle sum property of triangle]
⇒ 90° + 3 CP + ∠POA = 180°
⇒ ∠POA = 60°

Question 11.
A cylindrical vessel 32 cm high and 18 cm as the radius of the base, is filled with sand. This bucket is emptied on the ground and a conical heap of sand is formed. If the height of the conical heap is 24 cm, then the radius of its base is
(a) 30 cm
(b) 36 cm
(c) 34 cm
(d) 35 cm
Answer:
(b) 36 cm

Explanation:
Given cylindrical vessel having radius,
r = 18 cm and height, h = 32 cm
Also given, height of conical heap, H = 24 cm
Now, volume of cylindrical vessel = πr²h = π (18)² × 32
and volume of conical heap = \(\frac{1}{3}\) πR²H = \(\frac{1}{3}\) × π × R² × (24)
But according to the given condition,
Volume of cylindrical vessel = Volume of conical heap
∴ π(18)² × 32 = \(\frac{1}{3}\)πR² × 24
⇒ R = \(\frac{(18)^2 \times 3 \times 32}{24}\)
⇒ R² = (18)² × 4
⇒ R² =(36)²
⇒ R = 36 cm

Question 12.
The probability of 53 Monday in a non-leap year is
(a) \(\frac{1}{7}\)
(b) \(\frac{2}{7}\)
(c) \(\frac{6}{7}\)
(d) \(\frac{5}{7}\)
Answer:
(a) \(\frac{1}{7}\)

Explanation:
Total number of days in a non- leap year = 365
Number of weeks in a non-leap year = \(\frac{365}{7}\)
= 52 weeks and 1 day
Remaining day = 1 day
Total number of days in a week = 7
Probability of 53 Monday in a non-leap year
= \(\frac{\text { Remaining days }}{\text { Total number of days in a week }}=\frac{1}{7}\)

Question 13.
For some integer P, every even integer is of the form
(a) P
(b) P+ 1
(c) 2P
(d) 2P + 1
Answer:
(c) 2P

Explanation:
We know that, even integer are ……….-2,0, 2, 4, 6, ………..
So, it can be written in the form of 2 P.
Where, P=integer = Z [since, integer is represented by Z]
or P = ………..,-10, 1, 2, 3, ………….
2P = …………,-20, 2, 4, 6………

Question 14.
If the first three terms of an AP are x – 1, x + 1, 2x + 3, then the value of x is
(a) 1
(b) 2
(c) -1
(d) 0
Answer:
(d) 0

Explanation:
We have, x + 1 – (x – 1) = (2x + 3) – (x + 1)
[∵ common difference remains same]
⇒ 2 = x + 2
⇒ x = 0

Question 15.
If tan(θ₁ + θ₂) = √3 and sec(θ₁ – θ₂) = \(\frac{2}{\sqrt{3}}\), then the value of sin 2 θ₁ + tan 3θ₂ is
(a) 0
(b) 1
(c) 2
(d) 3
Answer:
(c) 2

Explanation:
Given, tan (θ₁ + θ₂) = √3
⇒ θ₁ + θ₂ = 60° …….(i)
Also, sec(θ₁ – θ₂) = \(\frac{2}{\sqrt{3}}\)
⇒ θ₁ – θ₂ = 30° ………(ii)

On adding Eqs. (i) and (ii), we get
2θ₁ = 90°⇒ θ₁ = 45°
Then, from Eq. (i), we get’
45°+ θ₂ = 6O° ⇒ θ₂ = 15°

Now, sin 2θ₁+ tan 3θ₂
= sin 90° + tan 45°
= 1 + 1 = 2

Question 16.
Find a point on X-axis which is equidistant from the points A(6, 4) and B (- 3, – 5).
(a) (\(-\frac{3}{2}\), 0)
(b) (0, 0)
(c) (1, 0)
(d) (-1, 0)
Answer:
(c) (1, 0)

Explanation:
Let the point C(x,0) be any point on the X-axis,
which is equidistant from points A(6,4) and B(- 3,-5).
∴ AC = BC …(i)

Now, distance between point A and C,
AC = \(\sqrt{(x-6)^2+(0-4)^2}\) [by distance formula]
⇒ AC = \(\sqrt{(x-6)^2+16}\)

and distance between point Band C,
BC = \(\sqrt{(x+3)^2+(0+5)^2}\)
⇒ BC = \(\sqrt{(x+3)^2+25}\)

Now, from Eq. (i), we get
\(\sqrt{(x-6)^2+16}=\sqrt{(x+3)^2+25}\)

On squaring both sides, we get
x² + 36 – 12x + 16 = x² + 9 + 6x + 25
⇒ – 18x + 52 – 34 = 0
⇒ x = 1
Hence, the point (1, 0) on X-axis, is equidistant from the points A(6, 4) and B(- 3, – 5).

Question 17.
If \(\frac{1}{2}\) is a root of the equation x + kx – \(\frac{5}{4}\) = 0, then the value of k is
(a) 2
(b) -2
(c) \(\frac{1}{4}\)
(d) \(\frac{1}{2}\)
Answer:
(a) 2

Explanation:
Given, \(\frac{1}{2}\) is a root of the quadratic equation x2 + kx – \(\frac{5}{4}\) = 0.
Then, (\(\frac{1}{2}\))² + k(\(\frac{1}{2}\)) – \(\frac{5}{4}\) = 0
⇒ \(\frac{1}{4}+\frac{k}{2}-\frac{5}{4}\) = 0
⇒ \(\frac{1+2 k-5}{4}\) = 0
⇒ 2k – 4 = 0
⇒ 2k = 4
⇒ k = 2

Question 18.
Find the length of arc, when arc subtends an angle of 90° at centre O of circle with radius of 10.5 cm.
(a) 16 cm
(b) 16.8 cm
(c) 17.2 cm
(d) 16.5cm
Answer:
(d) 16.5cm

Explanation:
Given, radius of circle = 10.5 cm
and angle subtended by arc at centre, θ = 90°
We know that the arc length = \(\frac{\theta}{360^{\circ}}\) × 2πr
⇒ Arc length = \(\frac{90^{\circ}}{360^{\circ}}\) × 2 × \(\frac{22}{7}\) × 10.5
= 16.5 cm

Assertion-Reason Based Questions
In the following questions, a statement of Assertion (A) is followed by a statement of Reason (R). Choose the correct answer out of the following choices.
(a) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
(b) Both Assertion (A) and Reason (R) are true but Reason (R) is not the correct explanation of Assertion (A).
(c) Assertion (A) is true but Reason (R) is false.
(d) Assertion (A) is false but Reason (R) is true.

Question 19.
Assertion (A) HCF of (11,17) is 1.
Reason (R) If pand qare prime, then HCF (p, q) = 1
Answer:
(a) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).

Explanation:
As both the given numbers (11,17) are prime numbers.
∴ HCF of (11, 17) = 1
Hence, both Assertion (A) and Reason (R) are true and
Reason (R) is the correct explanation of Assertion (A).

Question 20.
Assertion (A) Pair of linear equations 9x + 3y + 12 = 0 and 27x + 9y + 36 = 0 has infinitely many solutions.
Reason (R) Pair of linear equations a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₂ = 0 has infinitely many solutions, if
Answer:
(a) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).

Explanation:
Given equations are 9x + 3y+ 12 = 0 and 27x + 9y + 36 = 0
On comparing with the standard form of pair of linear equations a₁x + b₁y + c₁ =0 and a₂x + b₂y + c₂ = 0, we get a₁ =9. b₁ =3, c₁ =12 and a₂ =27, b₂ = 9, c₂ = 36
Here \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}=\frac{1}{3}\) …(i)
We know that pair of linear equations a₁x + bx₁ + c₁ = 0
and a₂x + b₂y + c₂ = 0 has infinitely many solutions, if
\(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\)
So, from Eq. (i) the given pair of linear equations has infinitely many solutions.
Hence, both Assertion and Reason are true and Reason is the correct explanation of Assertion.

Section – B
Very Short Answer Type Questions (Each Question carries 2 M)

Question 21.
In ∆ABC, right angled at B, if tan A = \(\frac{1}{\sqrt{3}}\), then find the value of
(i) sin A cos C + cos A sin C
(ii) cos A cos C – sin A sin C.
Answer:
Given, tan A = \(\frac{1}{\sqrt{3}}\)
⇒ tan A = tan 30° [∵ tan 30° = \(\frac{1}{\sqrt{3}}\)]
⇒ ∠A = 30° …..(i)

On applying angle sum property in right angled AABC, we get
∠A + ∠B + ∠C = 180°
⇒ 30°+ 90° + ∠C = 180°
[∵ from Eq. (i) and given, ∠B = 90°]
⇒ ∠C= 180° – 120°
⇒ ∠C = 60° …(ii)

(i) sin A cos C + cos A sin C = sin 30° cos 60° + cos 30° sin 60° [from Eqs. (i) and (ii)]
= \(\frac{1}{2} \times \frac{1}{2}+\frac{\sqrt{3}}{2} \times \frac{\sqrt{3}}{2}\)
[∵ sin 30° = \(\frac{1}{2}\), cos 60° = \(\frac{1}{2}\), cos 30° = \(\frac{\sqrt{3}}{2}\) and sin 60° = \(\frac{\sqrt{3}}{2}\)]
= \(\frac{1}{4}+\frac{3}{4}=\frac{4}{4}\)
= 1

(ii) cos A cos C – sin A sin C = cos 30° cos 60° – sin 30° sin 60° [from Eqs. (i) and (ii)]
= \(\frac{\sqrt{3}}{2} \times \frac{1}{2}-\frac{1}{2} \times \frac{\sqrt{3}}{2}\)
[∵ sin 30° = \(\frac{1}{2}\),cos 60° = \(\frac{1}{2}\),cos 30° = \(\frac{\sqrt{3}}{2}\) and sin 60° = \(\frac{\sqrt{3}}{2}\)]
= \(\frac{\sqrt{3}}{4}-\frac{\sqrt{3}}{4}\)
= 0

Question 22.
(a) Shivangi started work in 1991 at an annual salary of ? 5000 and received an increment of ₹ 200 each . year. In which year did her income reach ₹ 7000?
Or
(b) If five times the fifth term of an AP is equal to 8 times its eight term, show that its 13th term is zero.
Answer:
(a) The annual salary received by Shivangi in the years 1991,1992, 1993 etc., is ₹ 5000, ₹ 5200, ₹ 5400, ₹ 7000
Here, a₂ – a₁ = a₃ – a₂ = 200
Hence, the list of numbers 5000, 5200, 5400, 7000 form an AP.
Common difference, d = 200
Let nth term of an AP,
a_n = 7000
⇒ 7000 = a₁ + (n – 1)d [∵ a_n = a + (n – 1)d]
⇒ 7000 = 5000 + (n – 1) (200)
⇒ 200 (n – 1) = 7000 – 5000 = 2000
⇒ n – 1= \(\frac{2000}{200}\) = 1o
⇒ n = 10 + 1 = 11
Thus, in 11th yr of her service or in 2001, Shivangi received an annual salary ₹ 7000.

Or

(b) Let first term and common difference of an AP be a₁ and d, respectively.
According to the given condition,
5a₅ = 8a₈
⇒ 5[a₁ + (5 – 1)d] = 8[a₁ + (8 – 1)d] [∵ a_n =a + (n – 1)d]
⇒ 5[a₁ + 4d] = 8[a₁ + 7d]
⇒ 5a₁ + 20d = 8a₁ + 56d
⇒ 3a₁ + 36 d = 0
⇒ 3(a₁ + 12d) = 0
⇒ [a₁ + (13 – 1) d] = 0
⇒ a₁₃ = 0
Hence proved.

Question 23.
Find the area of minor segment AYR if radius of circle is 35 cm and ∠AOB = 90°.
Answer:
Given, r = 35 cm and ∠AOB = 90°
∴ Area of the sector OAYB= \(\frac{90^{\circ}}{360^{\circ}} \times \frac{22}{7}\) × 35 × 35
[∵ area of sector = \(\frac{\theta}{360^{\circ}}\) × πr²]
= 962.5 cm²

Area of ΔAOB = \(\frac{1}{2}\) × AO × OB
[∵ area of right angle triangle = \(\frac{1}{2}\) × base × perpendicular]
= \(\frac{1}{2}\) × 35 × 35 [∵ OA = OB = radius]
= 612.5 cm²

Now, area of minor segment AYB
= Area of sector OAYB – Area of ∆AOB
= 962.5 – 612.5
= 350 cm²

Question 24.
In ∆PQR, points X and Y are on PQ and QR, respectively, such that QX = 20 cm, QY = 8 cm, QP = 35 cm and QR = 14 cm. Is XY ∥ PR?
Answer:
Given, QX = 20 cm, QY = 8 cm, QP = 35 cm and QR = 14 cm


By converse of basic proportionality theorem, we get XYHPK.

Question 25.
(a) If PQ is a tangent to a circle with centre O at point P. If ∆OPQ is an isosceles triangle, then find ∠OQP.
Answer:
Given, PQis a tangent to a circle with centre Oand ∆OPQis an isosceles triangle.
Here, PO = PQ ⇒ ∠O = ∠Q …(i)
[∵ OP ⊥ PQ so OQ will be the longest side (hypotenuse) and hence, PO = PQ]

In ∆OPQ
∠P + ∠Q + ∠O = 180°
[∵ sum of all angles of a triangle is 180°]
⇒ 2∠Q + ∠P = 180° [using Eq. (i)]
⇒ 2∠Q + 90P = 180° [∠P = 90°,∵ OP ⊥ PQ]
⇒ 2∠Q = 90°⇒ ∠Q = 45;
Hence, ∠OQP = 45°

Or

(b) PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T (see figure). Find the length of TP.

Answer:
Given, chord PQ = 8 cm
Radius, OP = 5 cm
Join Or. Let it intersect PQ at the point R. Then, ∆TPQis an isosceles triangle and TO is the angle bisector of ∠PTQ. So, OT is perpendicular to PQ and therefore, OT bisects PQ which gives PR = RQ = \(\frac{P Q}{2}\) = 4 cm.

Also, in right angled ∆ORP, OR = \(\sqrt{O P^2-P R^2}\)
= \(\sqrt{5^2-4^2}\) cm
= \(\sqrt{25-16}\) = 3cm

Now, ∠TPO = ∠TPR + ∠RPO = 90° = ∠TPR + ∠PTR
[∵ radius is perpendicular to the tangent at the point of contact and
∠TPR + ∠PTR = 180° – ∠TRP= 180° – 90° = 90]
So, ∠RPO = ∠PTR
Therefore, right angled ∆TRP is similar to the right angled ∆PRO by AA similarity. This gives \(\frac{T P}{P O}=\frac{R P}{R O}\)
i.e. \(\frac{T P}{5}=\frac{4}{3}\)
TP = \(\frac{20}{3}\) cm = 6.66 cm

Section – C
Short Answer Type Questions (Each Question carries 3 M)

Question 26.
Find the ratio in which the line 2x + y = 4 divides the join of A (2, – 2) and B(3, 7). Also, find the coordinates of the point of intersection.
Answer:
Let the line 2x + y – 4= 0 divides the line segment joining the points A (2, – 2) and B (3, 7) in the ratio fc: 1 at the point P.

∴ Coordinates of P = \(\left(\frac{3 k+2}{k+1}, \frac{7 k-2}{k+1}\right) .\)
Using section formula
i.e \(\left(\frac{m_1 x_2+m_2 x_1}{m_1+m_2}, \frac{m_1 y_2+m_2 y_1}{m_1+m_2}\right)\)
But P lies on the line 2x + y – 4 = 0.
So, coordinates of P satisfy the equation 2x + y – 4 = 0
∴ 2\(\left(\frac{3 k+2}{k+1}\right)\) + \(\frac{7 k-2}{k+1}\) – 4 = 0
⇒ 6k + 4 + 7k – 2 4k – 4 = 0
⇒ 9k – 2 = 0
⇒ 9k = 2
⇒ k = \(\frac{9}{2}\)
So, the point P divides the line segment in the ratio 2:9.
Now, coordinates of P = \(\left(\frac{3 \times \frac{2}{9}+2}{\frac{2}{9}+1}, \frac{7 \times \frac{2}{9}-2}{\frac{2}{9}+1}\right)\)
= \(\left(\frac{6+18}{2+9}, \frac{14-18}{2+9}\right)=\left(\frac{24}{11}, \frac{-4}{11}\right)\)

Question 27.
Prove that cot A\(\sqrt{\frac{1+\sin A}{1-\sin A}}=\frac{1+\sin A}{\sin A}\)
Answer:

Question 28.
(a) Solve the following equation for x, 9(x² + \(\frac{1}{x^2}\)) – 9(x + \(\frac{1}{x}\)) – 52 = 0. ‘
Answer:
Given, 9(x² + \(\frac{1}{x^2}\)) – 9(x + \(\frac{1}{x}\)) – 52 = 0
We know that
(x + \(\frac{1}{x}\))² = x² + \(\frac{1}{x^2}\) + 2
x² + \(\frac{1}{x^2}\) = (x + \(\frac{1}{x}\))² – 2

On putting x + \(\frac{1}{x}\) = y then x²² + \(\frac{1}{x^2}\) = y² – 2

The given equation becomes 9 (y² – 2) – 9y – 52 = 0
⇒ 9y² – 18 – 9y – 52 = 0
⇒ 9y² – 9y – 70 = 0
⇒ 9y² – 30y + 21y – 70 = 0
[by splitting the middle term]
⇒ 3y(3y – 10) + 7(3y – 10) = 0
⇒ (3y – 10)(3y + 7) = 0
⇒ 3y – 10 = 0 or 3y + 7 = 0
⇒ 3y = 10 or 3y = -7
⇒ y = \(\frac{10}{3}\) or y = –\(\frac{7}{3}\)
When y = \(\frac{10}{3}\) then x + \(\frac{1}{x}=\frac{10}{3}\)
⇒ 3x² + 3 = 10x
⇒ 3x² – 9x – x + 3 = 0
[by splitting the middle term]
⇒ 3x(x – 3) -1(x – 3) = 0
⇒ (x – 3)(3x – 1) = 0
⇒ x – 3 = 0 or 3x – 1 = 0
⇒ x – 3 or 3x = 1
⇒ x = 3 or x = \(\frac{1}{3}\)

When, y = \(-\frac{7}{3}\) then x + \(\frac{1}{x}=-\frac{7}{3}\)
⇒ 3x² + 3 = – 7x
⇒ 3x² + 7x + 3 = 0
On comparing Eq. (i) with ax² + bx + c = 0, we get
a = 3, b = 7 and c = 3
D = b² – 4ac
= (7)² – 4 × 3 × 3
= 49 – 36 = 13 > 0
So, real roots exist, which are given by using quadratic formula,
x = \(\frac{-b \pm \sqrt{D}}{2 a}=\frac{-7 \pm \sqrt{13}}{2 \times 3}=\frac{-7 \pm \sqrt{13}}{6}\)
Hence, x = 3, \(\frac{1}{3}\) and \(\frac{-7 \pm \sqrt{13}}{6}\)

Or

(b) Using quadratic formula, solve for x, 9x² – 3(a + b)x + ab = 0.
Answer:
Given equation is 9x² – 3(a + b)x + ab = 0.
On comparing with Ax² + Bx + C=0, we get
A = 9, B = -3(a + b) and C = ab
Discriminant,
D= B² -4AC
= 9(a + b)² -4(9)(ab)
= 9{(a + b)² – 4ab}
= 9(a – b)² > 0 [∵ (a + b)² – 4ab = (a – b)²]
Therefore, the two real roots of the equation are given by

Hence, the two roots are \(\frac{a}{3}\) and \(\frac{b}{3}\).

Question 29.
(a) Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
Answer:
Let AB be a diameter of a given circle and LM and PQ be the tangent lines drawn to the circle at points A and B, respectively.

To prove
LM ∥ PQ
We know that the tangent at any point of a circle is perpendicular to the radius through the point of contact.
∴ OA ⊥ PQ and OB ⊥ LM
⇒ AB ⊥ PQ and AB ⊥ LM
∠PAB = ∠ABM = 90°
But these are alternate angles.
∴ PQ ∥ LM
Hence, the tangents drawn at the ends of a diameter of a circle are parallel.
Hence proved.

Or

(b) In the given figure, AB is diameter of a circle with centre Oand AT is tangent. If ∠AOQ= 70°, find ∠ATQ.

Answer:
Given, ∠AOQ = 70°
Also, ∠AOQ = 2∠ABQ
⇒ ∠ABQ = \(\frac{1}{2}\)∠AOQ
[∵ angle subtended by an arc at the centre is twice the angle subtended by it at remaining part of the circle.]
∴ ∠ABQ= 35°
and ∠BAT = 90°
[∵ radius is perpendicular to tangent at the point of contact]

In ∆ABT,
∠ABT + ∠BTA + ∠BAT = 180°
[∵ sum of all the angles of a triangle is 180°]
⇒ 35° + ∠ATQ + 90° = 180°
[∵ ∠BTA = ∠ATQ]
⇒ ∠ATQ= 180° – 125°
⇒ ∠ATQ = 55°

Question 30.
Three sets of English, Hindi and Mathematics book have to be stacked in such a way that all the books are stored topicwise and the height of each stack is the same.
The number of English books is 96, the number of Hindi books is 240 and the number of Mathematics books is 336. Assuming that the books are of the same thickness, determine the number of stacks of English, Hindi and Mathematics books.
Answer:
In order to arrange the books as required, we have to find the largest number that divides 96, 240 and 336 exactly. Therefore, such a number is their HCF.
Now, 96 = 2⁵ × 3,
240 = 2⁴ × 3 × 5
and 336 = 2⁴ × 3 × 7
∴ HCF of (96, 240, 336) = 2⁴ × 3 = 48
So, there must be 48 books in each stack.
Now, number of stacks of English books = \(=\frac{240}{48}\frac{96}{48}\) = 2
Number of stacks of Hindi books = \(\frac{240}{48}\) = 5
and number of stacks of Mathematics books = \(\frac{336}{48}\) = 7

Question 31.
If the 3rd and 8th terms of an AP are 11 and 36, respectively. Then, find the ratio of sum of 7 terms and sum of 11 terms of that AP.
Answer:
Let a and d be first term and common difference of the AP, respectively.
Given, 3rd term = a + 2d = 11 ..(i) [∵ a_n = a + (n – 1)d]
and 8th term = a + 7d = 36 …(ii)
On subtracting Eq. (i) from Eq. (ii), we get
5d = 25
⇒ d = 5 …(iii)
On putting d = 5, in Eq. (i), we get
a+ 10 = 11
⇒ a = 1 …(iv)
We know that the sum of n terms of an AP is
S_n = \(\frac{n}{2}\)[2a + (n – 1)d]

Now, sum of 7 terms of AP = \(\frac{7}{2}\) [2 × 1 + (7 – 1)5]
[using Eqs. (iii) and (iv)]
⇒ S₇ = \(\frac{7}{2}\)[2+30]
⇒ S₇ = \(\frac{7}{2}\) × 32
⇒ S₇ = 112

Sum of 11 terms of AP = \(\frac{11}{2}\)[2 × 1 + 10 × 5]
⇒ S₁₁ = 11 × 26
⇒ S₁₁ = 286
Now, ratio of sum of 7 terms and sum of 11 terms of the
AP, \(\frac{S_7}{S_{11}}=\frac{112}{286}=\frac{56}{143}\)
Hence, the ratio of sum of 7 terms and sum of 11 terms of the AP is 56 :143.

Section – D
Long Answer Type Questions (Each Question carries 5 M)

Question 32.
(a) Find the mean of the following frequency distribution using assumed mean method.

Answer:
Let us make the following table.

Here, assumed mean, A = 17,
Σf_i = 40 and Σf_id_i = 72
∴ Mean (x̄) = A + \(\frac{\Sigma f_i d_i}{\Sigma f_i}\)
= 17 + \(\frac{72}{40}\)
= 17 + 1.8
= 18.8

Or

(b) The following frequency distribution gives the monthly consumption of electricity of 68 consumers of a locality. Find the median of the data.

Monthly consumption (in units)	Number of consumers
65-85	4
85-105	5
105-125	13
125-145	20
145-165	14
165-185	8
185-205	4

Answer:
Table for cumulative frequency is given below.

Monthly consumption (in units)	Number of consumers (fi)	Cumulative frequency (cf)
65-85	4	4
85-105	5	9
105-125	13	22 (cf)
125-145	20(f)	42
145-165	14	56
165-185	8	64
185-205	4	68
Total	N = 68

Here, number of observations, N = 68
Since, cumulative frequency just greater than 34 is 42 and the corresponding class interval is 125-145.
Therefore, 125-145 is the median class.
Here, lower limit of median class, l = 125,
frequency of median class, f = 20,
cumulative frequency of class preceding the median class, cf = 22
and class size, h = 145 – 125 = 20

Hence, the median of the given data is 137.

Be careful when calculating total number of consumers and cumulative frequency.

Question 33.
A rocket is in the form of a right circular cylinder closed at the lower end and surmounted by a cone with the same radius as that of the cylinder. The diameter and height of the cylinder are 6 cm and 12 cm, respectively.
If the slant height of the conical portion is 5 cm, then find the total surface area and volume of the rocket, (take π = 314)
Answer:
Given, rocket is the combination of a right circular cylinder and a cone.
Diameter of the cylinder = 6cm
∴ Radius of th cylinder = \(\frac{6}{2}\) = 3 cm
and height of the cýlinder = 12cm

∴ Volume of the cylinder = πr²h
= 3.14 × (3)² × 12
= 339.12 cm³

Curved surface area of cylinder = 2πrh
= 2 × 3.14 × 3 × 12
= 226.08 cm²

and area of base of cylinder = πr²
= 3.14 × 3 × 3
= 28.26 cm²

Now, in right angled AAOC,
h = \(\sqrt{5^2-3^2}=\sqrt{25-9}=\sqrt{16}\) [∵ l = 5 cm]
.’. Height of the cone, h = 4 cm
and radius of the cone, r = 3 cm
Now, volume of the cone = \(\frac{1}{3}\)πr²h
= \(\frac{1}{3}\) × 3.14 × (3)² × 4
= 3.14 × 3 × 4
= 37.68 cm³

and curved surface area of cone = πrl
= 3.14 × 3 × 5
= 47.1 cm²

Hence, total volume of the rocket
= Volume of the cylinder + Volume of the cone
= 339.12 + 37.68
= 376.8 cm³

and total surface area of the rocket
= Curved surface area of cone + Curved surface area of cylinder + Area of base of cylinder
= 47.1+226.08 + 28.26
= 301.44 cm²

Question 34.
(a) Solve graphically the pair of linear equations x – y + 1 = 0 and 3x + 2y – 12 = 0. Determine the coordinates of the vertices of the triangle formed by these lines and the X-axis and shade the triangular region.
Answer:
Given, pair of linear equations is x – y + 1 = 0 and 3x + 2y-12 = 0.
Table for x – y + 1 = 0 or y = x + 1 is

X	0	4	-1
Y = x + 1	1	5	0
Points	A(0, 1)	B(4, 5)	c (-X, 0)

Table for 3x + 2y – 12 = 0 or y = \(\frac{12-3 x}{2}\) is

X	0	2	4
Y = \(\frac{12-3 x}{2}\)	6	3	0
Points	D (0,6)	E (2, 3)	F (4,0)

Now, plot the points A (0, 1), B(4, 5), C (-1, 0) and join them to get a line CB.
Similarly, plot the points D(0, 6), E(2, 3), F (4, 0) and join them to get a line DF.

Clearly, the two lines intersect each other at the point E (2, 3). Hence, x = 2 and y = 3 is the solution of the given pair of equations. The line DE cuts X-axis at the point F (4, 0) and the line AB cuts X-axis at the point C(-1, 0).
Hence, the coordinates of the vertices of the AEFC, so formed are E(2, 3), F(4, 0) and C(-2, 0).

Or

(b) The area of a rectangle gets reduced by 9 sq units, if its length is deduced by 5 units and breadth is increased by 3 units. If we increase the length by 3 units and the breadth*by 2 units, then the area increased by 67 sq units. Find the dimensions of the rectangle.
Answer:
Let x units be the length and y units be the breadth of a rectangle then area of rectangle = xy sq units.
In first case Area is reduced by 9 sq units, when length = (x – 5) units and breadth = (y + 3) units
Then, area of rectangle = (x – 5)(y + 3) sq units
According to the question,
xy – (x – 5) x (y + 3) = 9
⇒ xy – (xy + 3x – 5y – 15) = 9
⇒ -3x + 5y + 15 = 9
⇒ 3x – 5y = 6 …(i)

In second case Area is increased by 67 sq units, when length = (x + 3) units and breadth = (y + 2) units
According to the question,
(x + 3) x (y + 2) – xy = 67
⇒ xy + 2x + 3y + 6 – xy = 67
⇒ 2x + 3y = 61 ……..(ii)

On multiplying Eq. (i) by 3 and Eq. (ii) by 5, we get
9x – 15y = 18 …..(iii)
and 10x + 15y = 305 ………(iv)

On adding Eqs. (iii) and (iv), we get
19x = 323 ⇒ x = 17
On substituting x = 17 in Eq. (ii), we get
34 + 3y = 61
⇒ 3y = 27
⇒ y = 9
Hence, the length of the rectangle is 17 units and breadth of the rectangle is 9 units.

Question 35.
In the given figure, AP = 6 cm, AR = 9 cm, AQ = 12 cm, AB= 10 cm and AC = 20 cm, then find AD.

Answer:
Given, AP = 6 cm, AR = 9 cm, AQ = 12 cm, AB = 10 cm and AC = 20 cm
Here, \(\frac{A P}{A B}=\frac{6}{10}=\frac{3}{5}\)
and \(\frac{A Q}{A C}=\frac{12}{20}=\frac{3}{5}\)
\(\frac{A P}{A B}=\frac{A Q}{A C}=\frac{3}{5}\)
Then PQ ∥ BC
[by converse of basic proportionality theorem]
In ∆ARQ and ∆ADC,
∠RAQ = ∠DAC [common angle]
∠ARQ = ∠ADC [corresponding angles]
and ∠RQA = ∠DCA [corresponding angles]
So, AARQ ~ AADC [by AAA similarity criterion]
\(\frac{A R}{A D}=\frac{A Q}{A C}\)
[since, corresponding sides of similar triangles are proportional]
\(\frac{9}{A D}=\frac{12}{20}\)
[∵ AR = 9 cm, AQ = 12 cm and AC = 20 cm]
⇒ AD = \(\frac{9 \times 20}{12}\)
⇒ AD = 15 cm

Section – E
Case-Study/Passage-Based (Each Question carries 4 M)

Question 36.
The revenue (in ₹) of a firm is represented by the polynomial R(x) = 5x² +4x + 7, and the expenditure (in ₹) by the firm is represented by the polynomial E(x) = 3x² – 2. Where x is the number of items produced by the firm in a year.
On the basis of above information, answer the following questions. [1]
(i) Find the profit polynomial p(x). [1]
(ii) If the firm produces T000 products in a year, find the revenue and profit (in ₹) for the firm using the polynomials. [1]
(iii) (a) If tax is calculated on the profit using the polynomial T(y) = 0.3y + 100, where y represents the profit earned. Then, find the tax that firm paid. [2]
Or
(b) If tax is calculated oathe profit using the polynomial G(y)= 0.005y + 50, where y represents the profit darned. Then, find the tax that firm paid. [2]
Answer:
Given, revenue R(x) = 5x² + 4x + 7,
Expenditure F(x) = 3x² – 2, where x = number of items produced

(i) We know that
Profit = Revenue – Expenditure
y = P(x) = 5x² + 4x + 7 – (3x² – 2)
= 5x² + 4x + 7 – 3x² + 2
= 2x² + 4x + 9 ……..(i)

(ii) It form produces 1000 products in a year.
Then, revenue, R(1000) = 5(1000)² + 4(1000) + 7
= 5 x 10⁶ + 4000 + 7
= ₹ 5004007

And profit, y = 2×1 + 4x + 9
=> y₁₀₀₀ = 2(1000)“ +4000+9
= ₹ 2004009

(vii) (a) Given, Tax, T(y) = 0.3y + 100
where, y = profit earned by the firm
Then, 7(2004009) = 0.3(2004009)+ 100
= ₹ 601302.7

Or

(b) Given, tax C(y) = 0.005y + 50
where, y represents the profit earned by the firm.
Then, C(2004009) = 0.005(2004009) + 50
= 10020.045 + 50
= ₹ 10070.045

Question 37.
At a local fair, three hot air balloons, X,Y,Z are flying along the same plane. At a particular instant, their positions and angle between them are as shown in the given diagram.

The horizontal distance between balloons X and Y is equal to Xs altitude.
Balloons X,r Y and Z are placed such that ZXYZ= 90°. ^
On the basis of above information, answer the following questions.
(i) Find the altitude of balloon Y.
(ii) Find the distance between balloons X and Y. toil
(iii) (a) Find the shortest distance between balloons Y and Z.
Or
(b) Find the shortest distance between balloons X and Z.
Answer:
Given, altitude of X = 1500 m.
And horizontal distance between balloons X and Y
= Altitude of X = 1500 m
∴ OX = 1500 m
The altitude of balloon Y = altitude of balloon X + OY
= 1500+ 1500
= 3000 m

Question 38.
Shruti wrote numbers from 2 to 7 on six papers such that the number on each paper was unique. She divided the even and odd numbered papers into two groups, X and Y, respectively.
She then choose a paper from each group at random, one after the other, without looking, and used the numbers written on them to form a 2-digit number. The number chosen first is written at the tens place of the 2-digit number.
On the basis of above information, answer the following questions.
(i) Find the probability that Shruti makes an even number less than 20. [1]
(ii) (a) Shruti thought she is more likely to form an even number greater than 40 as compared to an odd number less than 40. Is she correct? [2]
Or
(b) What is the probability that Shruti makes number more than 30 but less than 50. [2]
(iii) Shruti redistributed the 6 papers evenly between two new groups, A and B making sure each group had a mix of even and odd numbered papers.
Write one possible distribution of the papers in the two groups, group A and group B such that the probability of forming an odd number is higher than that of formation of an even number, if the paper from group A is chosen first. [1]
Answer:
We have, numbers on papers = {2, 3, 4,5, 6, 7}
Even number group, X = {2, 4, 6}
and odd number group, Y = {3, 5, 7}
As given condition, the numbers that can be formed, are S = {23, 25, 27, 43, 45, 47, 63, 65, 67, 32, 34, 36, 52, 54, 56, 72, 74, 76}
Total numbers that can be formed, n( S) = 18

(i) Smallest even number that can be made = 32
and smallest number that can be made = 23
It is impossible for Shruti to make an even number less than 20.
And we know that probability of impossible event is zero.
So, required probability is zero.

(ii) (a) Let E[ be the event of even numbers greater than 40 and Eq be the event of odd numbers less than 40.
∴ E₁ = {52,54, 56, 72, 74, 76}
and E₂ = {23, 25, 27}
⇒ n(E₁) = 6 and n(E₂) = 3
Now, probability that Shruti makes an even
number greater than 40, P( E₁) = \(\frac{6}{18}=\frac{1}{3}\).
And probability that Shruti makes an odd
number less than 40, P(E₂) = \(\frac{3}{18}=\frac{1}{6}\).

As we seen, P(E₁) > P(E₂)
Therefore, Shurti is correct.

(b) Let E₃ be the event of numbers more than 30 but less than 50.
Then, E₃ = {32, 34, 36, 43, 45, 47}
⇒ n(E₃) = 6
∴ Probability that Shruti makes a number more than 30 but less than 50, P(E₃) = \(\frac{6}{18}=\frac{1}{3}\)

(iii) Let one such redistribution of papers be Group A 2,4, 7 Group B 3,5, 6
As given condition that group-A is chosen first.
Then, formed numbers are
{23, 25, 26,43, 45, 46, 73, 75, 76}
⇒ n(S) = 9
Even numbers of this sample space = {26, 46, 76}
and odd numbers of this sample space = {23, 25, 43, 45, 73, 75}
Now, probability of forming an odd number.
P(odd)= \(\frac{6}{9}=\frac{2}{3}\) [∵ n(odd) = 6]
and probability of forming an even number 3 1
P(even) = \(\frac{3}{9}=\frac{1}{3}\) [∵ n(even) = 3]
Here, P (odd) > P (even)
That satisfies the given condition.

The post CBSE Sample Papers for Class 10 Maths Standard Set 4 with Solutions appeared first on Learn CBSE.

📚 NCsolve - Your Global Education Partner 🌍

Empowering Students with AI-Driven Learning Solutions

Welcome to NCsolve — your trusted educational platform designed to support students worldwide. Whether you're preparing for Class 10, Class 11, or Class 12, NCsolve offers a wide range of learning resources powered by AI Education.

Our platform is committed to providing detailed solutions, effective study techniques, and reliable content to help you achieve academic success. With our AI-driven tools, you can now access personalized study guides, practice tests, and interactive learning experiences from anywhere in the world.

🔎 Why Choose NCsolve?

At NCsolve, we believe in smart learning. Our platform offers:

• ✅ AI-powered solutions for faster and accurate learning.
• ✅ Step-by-step NCERT Solutions for all subjects.
• ✅ Access to Sample Papers and Previous Year Questions.
• ✅ Detailed explanations to strengthen your concepts.
• ✅ Regular updates on exams, syllabus changes, and study tips.
• ✅ Support for students worldwide with multi-language content.

🌐 Explore Our Websites:

🔹 ncsolve.blogspot.com
🔹 ncsolve-global.blogspot.com
🔹 edu-ai.blogspot.com

📲 Connect With Us:

👍 Facebook: NCsolve
📧 Email: ncsolve@yopmail.com

#NCsolve #EducationForAll #AIeducation #WorldWideLearning #Class10 #Class11 #Class12 #BoardExams #StudySmart #CBSE #ICSE #SamplePapers #NCERTSolutions #ExamTips #SuccessWithNCsolve #GlobalEducation